Note: problem difficulty is ranked using a star system.

• (*) One-star problems are fundamental to the unit, and can be done relatively quickly. Use these problems to introduce yourself to the material.

• (**) Two-star problems are more difficult, and require an understanding of one or two key concepts. Use these problems to test your understanding of the material.

• (***) Three-star problems are the most difficult, and require some creative thinking in addition to a deep familiarity with multiple key concepts. Use these problems to challenge yourself; if you can complete one of these, you’re on your way to mastering the material.

*Q6.1) You swing a yo-yo in a perfectly horizontal circle above your head (that is to say, the plane of the circle is parallel to the ground) so that it makes 10 revolutions in 5 seconds. If the yo-yo has a mass of 100g and the string is 80cm in length:

a) What’s the tension in the string?

b) If you were to let go of the string, what would be the yo-yo’s velocity at the instant you let go?

*Q6.2) If you were to swim in a perfect circle of radius 12 meters with a centripetal acceleration of 0.25m/s², how many revolutions would you complete in 10 minutes?

*Q6.3) A 300kg cart on a rollercoaster reaches a loop-de-loop of radius 10 meters. If the cart travels at 25m/s, what’s the magnitude and direction of the normal force acting on the cart when the cart is at:

a) the bottom of the loop?

b) the top of the loop?

*Q6.4) Assuming the Earth has a perfectly circular orbit, what’s the tangential speed of the Earth (relative to the Sun)? Note: the mass of the Sun is 1.99x10³⁰kg and the distance between the Earth and the Sun is 1.58x10⁸km.

**Q6.5) You glue a small pebble to the end of the 20cm-long minute-hand of a clock.

a) What’s the average acceleration (magnitude and direction) of the pebble from the instant that the minute hand points to the 12 until it points to the 6?

b) What’s the average acceleration (magnitude and direction) of the pebble from the instant that the minute hand points to the 12 until it points back at the 12 again after one complete revolution?

c) What’s the centripetal acceleration of the pebble?

**Q6.6) How long would a day on Earth need to be in order for a person at the surface to feel weightless? Note: the radius of Earth is 6 371km.

**Q6.7) Many communications satellites are placed in what is known as “geosynchronous orbit”. This means that they have an orbital period of exactly one day, and therefore always appear to be in the same spot in the sky. How high above Earth’s surface must such a satellite be located? Note: the mass of the Earth is 5.97x10²⁴kg and the radius of the Earth is 6 371km.

***Q6.8) You want to design a banked ramp for commuters to enter the freeway. What is the ideal angle of the bank (meaning, the angle that would require the least amount of course-correction from the drivers)? Assume that the speed limit on the ramp is 60km/h, that all drivers travel at the speed limit, and that the ramp is a circular arc with a radius of curvature of 400m. Note: Ignore the friction between the tires and the road.

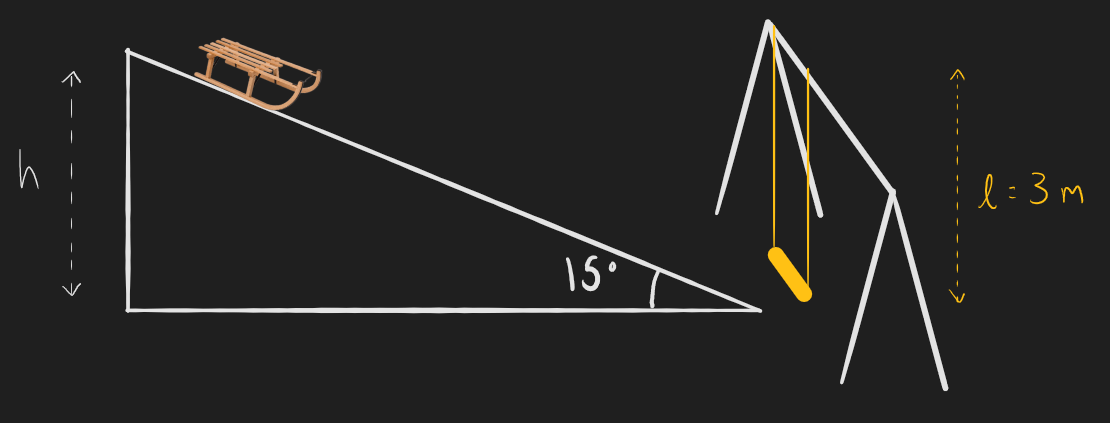
***Q6.9) Imagine that you want to toboggan down the hill shown below so that you can grab hold of the swing at the bottom and perform a perfect loop-de-loop.

a) From what minimum height must you be released from rest in order to make it all the way around the swing in a perfect loop? Ignore any friction between your toboggan and the snow.

b) From what minimum height must you be released from rest in order to make it all the way around the swing in a perfect loop assuming that the coefficient of kinetic friction between your toboggan and the snow is 0.2?

**Q6.10) To facilitate long journeys through space, simulated gravity would go a long way towards preventing deterioration of astronauts’ bodies. One way to simulate gravity in a spacecraft would be to rotate the spacecraft so that the centripetal acceleration is equal in magnitude to the acceleration due to gravity at Earth’s surface (g). If the crew cabin of a spacecraft is located 400 meters from the axis of rotation, what frequency of rotation would best simulate Earth’s gravity in the crew cabin?