Note: problem difficulty is ranked using a star system.

• (*) One-star problems are fundamental to the unit, and can be done relatively quickly. Use these problems to introduce yourself to the material.

• (**) Two-star problems are more difficult, and require an understanding of one or two key concepts. Use these problems to test your understanding of the material.

• (***) Three-star problems are the most difficult, and require some creative thinking in addition to a deep familiarity with multiple key concepts. Use these problems to challenge yourself; if you can complete one of these, you’re on your way to mastering the material.

*Q15.1) A sound wave travels in the (+) x-direction and is described by the equation y = 5sin( 6πt - 8πx ). The wave reflects off a wall that is perpendicular to its direction of propagation, causing it to travel in the (-) x-direction. The reflected wave then interferes with the incident wave, producing a standing wave.

a) Write the equation that describes the reflected wave.

b) Write the equation that describes the standing wave.

***Q15.2) Show that a standing wave can be described by the equation y = 2Acos(ωt)sin(kx). Hint: Start by considering the interference of two identical travelling waves (y = Asin(ωt ± kx)) moving in opposite directions.

**Q15.3) Many wind instruments are effectively tubes that are open at both ends, as shown below. Sketch the wave with the largest wavelength that will produce resonance inside the tube shown below.

**Q15.4) Some wind instruments are effectively tubes that are open at one end and closed at the other, as shown below. Sketch the wave with the largest wavelength that will produce resonance inside the tube shown below.

**Q15.5) String instruments can be thought of as tubes that are closed at both ends (in that the resonant standing wave has nodes at both ends). Sketch the wave with the largest wavelength that will produce resonance inside the tube shown below.

**Q15.6) Sketch the 2nd and 3rd longest waves that will cause resonance in each of the three tubes from Q15.3, Q15.4, and Q15.5, as shown below.

**Q15.7) Consider a guitar string of length 80cm. What are the frequencies of the 1st, 2nd, and 8th harmonics of this string?

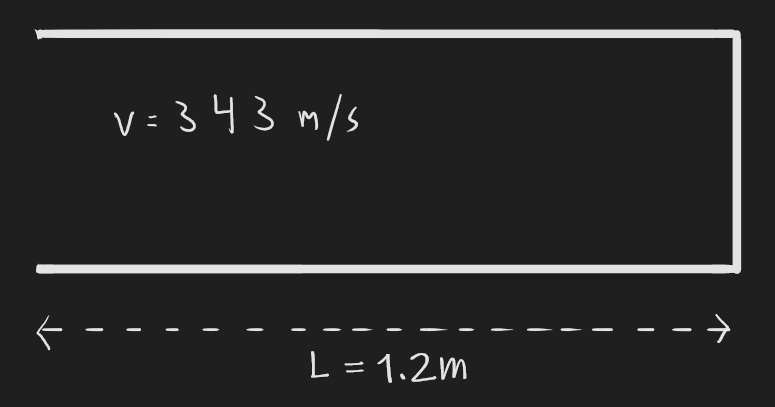
**Q15.8) Consider a tube of length 1.2m that is closed at one end and open at the other, similar to Q15.4. If sound travels with a speed of 343m/s inside the tube, find the frequency of the 1st, 3rd, and 15th harmonics of this tube.

**Q15.9) Consider a tube that is open at both ends and is of unknown length. If its 7th harmonic has a frequency of 3250Hz, what’s the frequency of its 11th harmonic?

***Q15.10) Consider a tube that is open at one end and closed at the other, as shown below. The closed end is sealed by a plunger that can be pulled out or pushed in, allowing for variance in the length of the tube. A tuning fork is placed near the opening of the tube and struck, sending sound of a certain frequency into the tube. As you lengthen the tube by pulling on the plunger, you notice that the sound is loudest (resonant) when the plunger is at certain positions along the tube. You take out a ruler and measure precisely 12cm between adjacent resonances. Find the frequency of the tuning fork.